Abstract
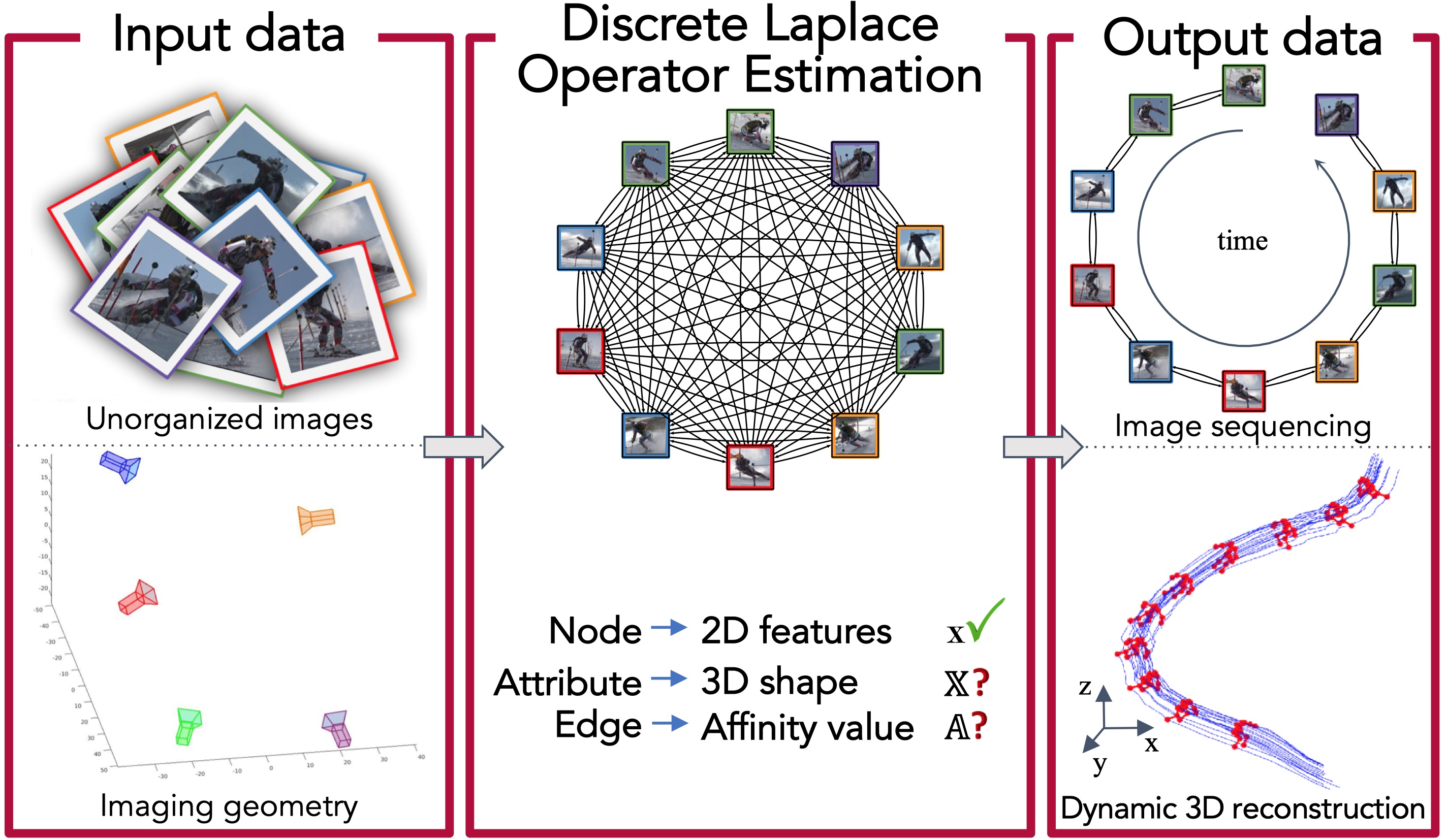
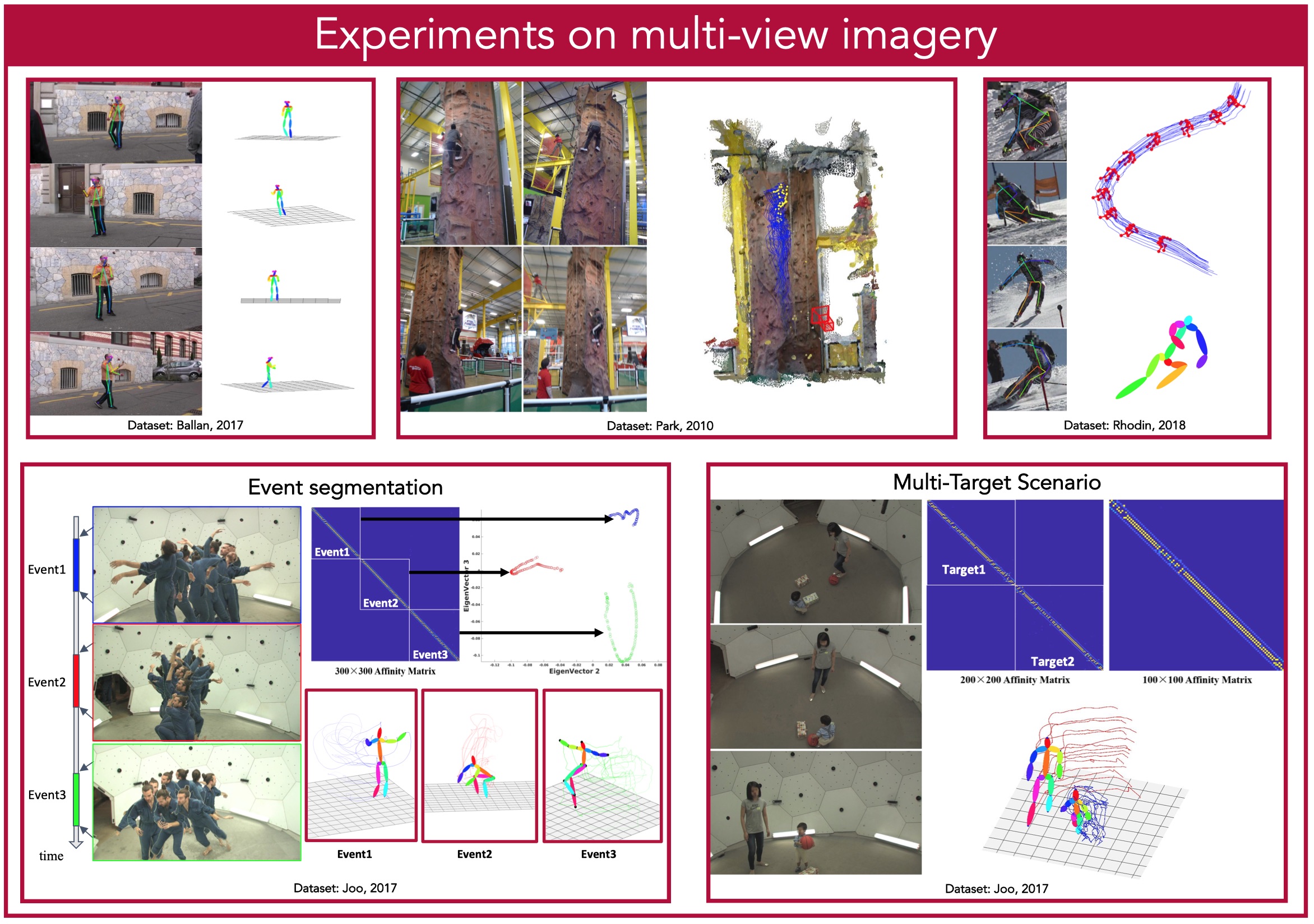
We present a general paradigm for dynamic 3D reconstruction from multiple independent and uncontrolled image sources having arbitrary temporal sampling density and distribution. Our graph-theoretic formulation models the spatio-temporal relationships among our observations in terms of the joint estimation of their 3D geometry and its discrete Laplace operator. Towards this end, we define a tri-convex optimization framework that leverages the geometric properties and dependencies found among a Euclidean shape-space and the discrete Laplace operator describing its local and global topology. We present a reconstructability analysis, experiments on motion capture data and multi-view image datasets, as well as explore applications to geometrybased event segmentation and data association.
Experiments
Resource
Publication(Accepted at ICCV 2019 as an oral presentation)
X. Xu and E. Dunn. Discrete Laplace operator estimation for dynamic 3D reconstruction. In Proceedings of the IEEE International Conference on Computer Vision, pages 1548-1557, 2019 (Oral)